Pressure and Density Altitude
There are many occasions in which a pilot has to predict the performance of an aircraft—e.g., in planning a takeoff, in planning a climb over mountainous terrain, in predicting rates of fuel consumption, and aircraft performance with respect to speed.
Generally, aircraft performance—in terms of lift generated by the wing, and thrust generated by the engine—decreases with an increase in ambient temperature and a decrease in ambient air pressure.
The concept of pressure altitude allows us to take into consideration any variation in the ambient pressure. We know that standard pressure—the pressure most likely to be encountered—is 29.92”Hg (inches of mercury) at sea level. We also know that the pressure of the air normally decreases 1”Hg with an 1000’ increase in altitude. Therefore, if we are at an airport with sea level elevation, and the current altimeter setting is 28.92”Hg, we can predict that the aircraft during the takeoff, for example, will perform as if it is doing the same takeoff at an airport with an elevation of 1000’, and performance will be degraded accordingly. Conversely, if the altimeter setting were 30.92”Hg—i.e., the pressure of the air is higher than normal or standard—the takeoff performance of the aircraft would be enhanced—as if the takeoff were conducted at an airport situated 1000’ under sea level where thick dense air (not water!) would provide better conditions for lift from the wing surfaces and thrust from the propeller and engine.
Calculation of pressure is done by calculating the difference between the current altimeter setting and the standard altimeter setting. This difference is then converted into feet, based on the given that 1”Hg = 1000’—this is referred to as the Standard Pressure Lapse Rate. Accordingly, if the current altimeter setting is 30.12”Hg., we would calculate as follows: 30.12 – 29.92 = .2. Using the standard lapse rate, .2 is converted into 200’. What do we do with this 200’? The answer is that if we want to determine the pressure altitude for an airport, we must add or subtract the 200’ relative to the airport’s elevation. If we want to determine the pressure altitude of an intended altitude that we want to cruise at, we must add or subtract the 200’ relative to the planned cruising altitude. The question of adding or subtracting the “correction value” is determined by whether the current air pressure is higher or lower than standard. Since pressure decreases with altitude, and the current altimeter setting is higher than standard, we should subtract the 200’. Thus, if the airport elevation were 3427’, we can say that the airport’s pressure altitude is 3227’ for the purpose of determining takeoff performance, and if the planned cruising altitude were 6500’ we know that when we level off with 6500’ indicated on the altimeter, the aircraft will burn fuel and produce an indicated airspeed as if it had levelled off at 6300’.
While pressure altitude provides a correction for pressure, it does not take into consideration the ambient temperature of the air—a factor that, on a hot day when performance of the aircraft is degraded, is far more critical.
In factoring in the influence of temperature on aircraft performance we shift to the concept of density altitude—that is, the higher the temperature, the higher the density altitude. Here we must use math, and the formula is as follows:
Density Altitude = Pressure Altitude + (100 ´ [actual temperature – standard temperature] )
Okay, how you are asking “what the heck is ‘standard temperature’”. The standard temperature at sea level is 15° C, and the standard temperature lapse rate is 2°/1000’ (actually 1.98° per 1000’, but the .02 that is missing never hurt anyone). (The origin of the standard temperature lapse rate is discussed on Page 140) What then is the standard temperature for an airport with an elevation of 2000’? The answer is 11° C as, we know, temperature will decrease 2° C for every 1000’ increase in altitude (15-4=11).
So we can see by the formula that density altitude will equal pressure altitude when the actual temperature is in fact the standard temperature for a given elevation or cruising altitude. What is the standard temperature for an airport with an elevation of 4000’? The answer is this: 4 ´ 2 = 8 and 15 – 8 = 7, or 7° C.
Now we can go into action: What is the density altitude of an airport with an elevation of 4,500’ when the altimeter setting is 28.92”Hg., and the temperature is 28° C.?
Density Altitude = Pressure Altitude + (100 ´ [28 – (15 - 9)])
Density Altitude = 5,500’ + (100 ´ [28 – 6)])
Density Altitude = 5,500’ + 2,200
Density Altitude = 7,700’
You can see how, with only a moderate increase in temperature, the performance of an aircraft can be extremely degraded—and a white-knuckle takeoff is truly something to avoid! For this reason, Pilot Operating Handbooks publish various tables that enable a pilot to calculate performance characteristics at varying temperatures and altitudes.
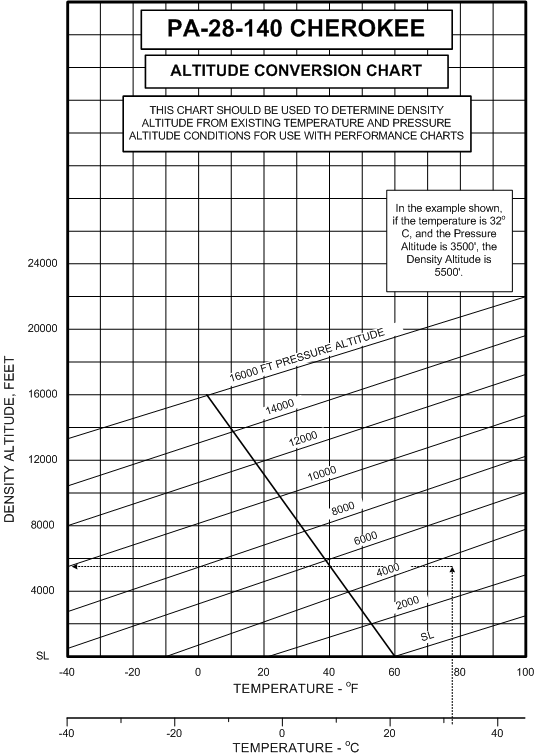
Instead of memorizing the above formula, consider the good news—density altitude can be readily calculated by spinning the wheel on the E6B, and the temperature and pressure factors are normally built into the performance charts published by an aircraft manufacturer’s Pilot Operating Handbook. The graph that appears below is similar to that which appears on p. 9-1 of the Cherokee manual. This graph is entered on the bottom with temperature (either in °F or °C—you E6B, by the way, is equipped with a conversion scale). In the example shown on the graph, the temperature is 32° C, and the pressure altitude is 3500’—figures that are common for summer departures from airports such a Calgary International Airport. A reference line is extended straight up from the temperature scale to intercept the pressure altitude lines that run at an angle. From this intercept point, a horizontal reference line is made directly to the density altitude scale which lies on the left side of the graph. The density altitude for the departure is approximately 5500.’
.jpg)

